ВВЕДЕНИЕ
Теория обнаружения детерминированного сигнала в аддитивном стационарном гауссовом шуме [1–3] базируется на фундаментальном результате теории проверки статистических гипотез – правиле (критерии)
отношения правдоподобия [4]. Монотонно неубывающее отношение
правдоподобия () в этом случае есть достаточная статистика, задающая линейное обнаружение со статистикой – линейной функцией
входного сигнала. В дискретном случае (входной сигнал X – вектор,
значения которого есть отсчеты непрерывного сигнала) статистика формируется как скалярное произведение
= H XT,
в котором H – весовой вектор, определяемый уравнением BH = S; B –
корреляционная матрица шума; S – обнаруживаемый детерминированный сигнал. Вследствие линейности (m, ), математические ожидания m0= m H|0= 0 , m1= m H|1= H ST= S B ST1 ; дисперсии
T
=
T1= m H
(1)
0 1
H BH S B S
1.
Логарифм отношения правдоподобия l ( )
наружения – линейная функция.
= ln ( ) линейного обЛинейный обнаружитель реализуется в виде согласованного фильтра или корреляционного приемника [1, 2]. Отношение сигнал-шум на
выходе линейного обнаружителя
2 = m22
S B ST1 =
T
1 2
d
/
d
,
2
1
2 2;U – амплитуда сигнала; 2
S B S00 0 вх
d = U
/ ш
ш –
вх
дисперсия шума; S = US0,
B = шB0 . ЛиD
нейный обнаружитель имеет симметричную относительно побочной диагонали
рабочую характеристику D = (F), D,F –
вероятности обнаружения и ложной тревоги [1,5] (рис. 1–1). Преимущество одного линейного обнаружителя над другим
проявляется в том, что D1 >D во всей области значений вероятности ложной тревоги
F
0 < F < 1. Это следует из правил обнаружения: правило среднего риска предусматРис. 1. Рабочие
характеристики
ривает использование матрицы потерь, связанной со средними вероятностями ошибок, а не с вероятностями F и D; правило Неймана–Пирсона, в котором используется заданный уровень вероятности F, справедливо для всех значений F.
Крутизна собственной [5] рабочей характеристики согласованной
фильтрации
= =
D D
F
F
( )
(2)
есть отношение правдоподобия для статистики [1, 6]. Эффективность
обнаружения можно оценить, например, площадью под рабочей характеристикой
являющейся функцией отношения сигнал-шум d2. Функциональная зависимость эффективности от отношения сигнал-шум существует при
обнаружении известного сигнала на фоне гауссова шума и по общепринятым правилам [1–5].
Рабочая характеристика рассчитывается независимо от конкретных
правил обнаружения. Различным правилам соответствуют различные
рабочие точки на характеристике, пересчитываемые одна в другую. Это
обстоятельство позволяет использовать правило отношения правдоподобия, описывающегося в пространстве статистики рабочей характеристикой, как обобщенное правило обнаружения детерминированного
сигнала в гауссовом шуме.
В случае непрерывного сигнала интегральное уравнение

6. ОБЗОР СТЕГОАЛГОРИТМОВ ВСТРАИВАНИЯ ИНФОРМАЦИИ В ИЗОБРАЖЕНИЯ

По способу встраивания информации стегоалгоритмы можно разделить на линейные (аддитивные), нелинейные и другие. Алгоритмы аддитивного внедрения информации заключаются в линейной модификации исходного изображения, а ее извлечение в декодере производится корреляционными методами. При этом ЦВЗ обычно складывается с изображением-контейнером, либо «вплавляется» (fusion) в него. Эти алгоритмы будут рассмотрены в п.6.1. В нелинейных методах встраивания информации используется скалярное либо векторное квантование. Обзор соответствующих алгоритмов выполнен в п.6.2. Среди других методов определенный интерес представляют методы, использующие идеи фрактального кодирования изображений. Их обзор приведен в п.6.3.

 

6.1. Аддитивные алгоритмы

6.1.1. Обзор алгоритмов на основе линейного встраивания данных

 

В аддитивных методах внедрения ЦВЗ представляет собой последовательность чисел w_i длины N,  которая внедряется в выбранное подмножество отсчетов исходного изображения f. Основное и наиболее часто используемое выражение для встраивания информации в этом случае

 

                                 (6.1)

где – весовой коэффициент, а  — модифицированный пиксел изображения.

Другой способ встраивания водяного знака  был предложен И.Коксом  [11]:

                                    (6.2)

или, при использовании логарифмов коэффициентов

 

                                      (6.3)

При встраивании в соответствии с (6.1) ЦВЗ в декодере находится следующим образом:

 

.                                 (6.4)

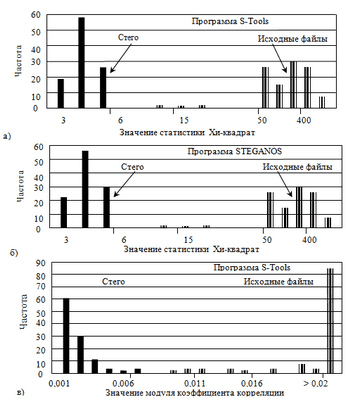
Здесь под f^* понимаются отсчеты полученного  изображения, содержащего или не содержащего ЦВЗ w. После извлечения  сравнивается с подлинным ЦВЗ. При чем в качестве меры идентичности водяных знаков используется значение коэффициента корреляции последовательностей

 

.                                              (6.5)

Эта величина варьируется в интервале [-1; 1]. Значения, близкие к единице, свидетельствуют о том, что извлеченная последовательность с большой вероятностью может соответствовать встроенному ЦВЗ. Следовательно,  в этом случае делается заключение, что анализируемое изображение содержит водяной знак.

В декодере может быть установлен некоторый порог, (здесь S – стандартное среднее квадратическое отклонение), который  определяет вероятности ошибок первого и второго рода при обнаружении ЦВЗ. При этом коэффициент  может не быть постоянным, а адаптивно изменяться в соответствии с

7. СКРЫТИЕ ДАННЫХ В АУДИОСИГНАЛАХ

 

Для того, чтобы перейти к обсуждению вопросов внедрения информации в аудиосигналы, необходимо определить требования, которые могут быть предъявлены к стегосистемам, применяемым для встраивания информации в аудиосигналы:

—            скрываемая информация должна  быть стойкой к наличию различных окрашенных шумов, сжатию с потерями, фильтрованию, аналогово-цифровому и цифро-аналоговому преобразованиям;

—            скрываемая информация не  должна  вносить в сигнал  искажения, воспринимаемые системой слуха человека;

—            попытка удаления скрываемой информации должна приводить к заметному повреждению контейнера (для ЦВЗ);

—            скрываемая информация не должна вносить заметных изменений в статистику контейнера;

Для внедрения скрываемой информации в  аудиосигналы можно использовать методы, применимые в других видах стеганографии. Например, можно внедрять информацию, замещая наименее значимые биты (все или некоторые). Или можно строить стегосистемы, основываясь на особенностях аудиосигналов и системы слуха человека.

Систему слуха человека можно представить, как анализатор частотного спектра, который может обнаруживать и распознавать сигналы в диапазоне 10 – 20000 Гц. Систему слуха человека можно смоделировать, как 26 пропускающих фильтров, полоса пропускания, которых увеличивается с увеличением частоты. Система слуха человека различает  изменения фазы сигнала слабее, нежели изменения амплитуды или частоты.

Аудиосигналы можно разделить на три класса:

—            разговор телефонного качества, диапазон 300 – 3400 Гц;

—            широкополосная речь 50 – 7000 Гц;

—            широкополосные аудиосигналы 20 – 20000 Гц.

Практически все аудиосигналы имеют характерную особенность. Любой из них представляет собой достаточно большой объем данных, для того, чтобы использовать статистические методы внедрения информации. Первый из описываемых методов, рассчитанный на эту особенность аудиосигналов, работает во временной области.

 

7.1. Методы кодирования с расширением спектра

 

Алгоритм, предложенный в работе [2], удовлетворяет большинству из предъявляемых требований, изложенных выше. ЦВЗ внедряется в аудиосигналы (последовательность 8- или 16-битных отсчетов) путем незначительного изменения амплитуды каждого отсчета. Для обнаружения ЦВЗ не требуется исходного аудиосигнала.

Пусть аудиосигнал состоит из N отсчетов x(i), i =1, …, N, где значение N не меньше 88200 (соответственно 1 секунда для стереоаудиосигнала, дискретизированного на частоте 44,1 кГц). Для того чтобы встроить ЦВЗ, используется функция f(x(i), w(i

3. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛОВ ПЕРЕДАЧИ

СКРЫВАЕМОЙ ИНФОРМАЦИИ

 

3. 1. Понятие скрытой пропускной способности

 

Для стеганографических систем важно определить, насколько большой может быть пропускная способность каналов передачи скрываемых сообщений и как она зависит от других характеристик стегосистем и условий их использования. Неформально определим, что под пропускной способностью каналов передачи скрываемых сообщений или просто скрытой пропускной способностью (ПС) будем понимать максимальное количество информации, которое может быть вложено в один элемент контейнера. При этом скрываемые сообщения должны быть безошибочно переданы получателю и защищены от атак нарушителя, таких как попытки обнаружения факта наличия канала скрытой связи, чтения скрываемых сообщений, преднамеренного ввода ложных сообщений или разрушения встроенной в контейнер информации. Канал скрытой связи образуется внутри канала открытой связи, для которого в работах К.Шеннона по теории информации определена пропускная способность [1]. Пропускная способность канала открытой связи определяется  как количество информации, которое потенциально можно передать без ошибок за одно использование канала. При этом не предъявляется никаких требований к защищенности от атак организованного нарушителя. Поэтому логично предположить, что скрытая пропускная способность должна быть меньше пропускной способности канала открытой связи, в котором за одно использование канала передается один элемент контейнера, в который вложена скрываемая информация.

Существуют различные подходы к определению количества информации, защищаемой от различных атак нарушителя стеганографическими методами. Эти различия, в частности, обусловлены различием в цели защиты информации, моделями нарушителя, его возможностями,  реализуемыми им атаками на стегосистемы, видом используемых контейнеров и скрываемых сообщений и многими другими факторами. Методами теории информации оценим для различных стегосистем величину пропускной способности каналов передачи скрываемой информации. Теоретико-информационные методы позволяют получить строгие оценки количества скрываемой информации, и эти оценки могут быть использованы как теоретически достижимые верхние пределы скорости передачи скрываемой информации для стегосистем с произвольными принципами их построения.

Рассмотрим два основных подхода к оценке  пропускной способности каналов передачи скрываемой информации. Первый из них, развиваемый в работах [2,3], ориентирован на стегосистемы, в которых защищаемые сообщения должны быть безошибочно переданы в условиях активного противодействия нарушителя.  Этот подход описывает сценарий скрытия

3.12. Скрытая пропускная способность стегоканала
при пассивном нарушителе

В ранее рассмотренном подходе к определению скрытой ПС не рассматривается зависимость между ее величиной и характе-ристиками скрытности вложенных в контейнер сообщений. Это, в частности, объясняется тем, что в ряде стегосистем, таких как системы ЦВЗ или системы с идентификационными номерами, факт наличия аутентифицирующей информации в контейнере мо-жет и не скрываться от нарушителя. Соответственно, необнаруживаемость водяного знака нужна только с целью минимизации искажений контейнера с целью сохранения высокого качества заверяемых музыкальных, изобразительных или иных контейне-ров, а также с целью затруднения оценки нарушителем эффективности действий по удалению (разрушению) водяного знака. Иная ситуация в стегосистемах, в которых способность нарушителя выявлять факт передачи скрываемых сообщений классифицирует-ся как взлом системы.
Исследуем величину скрытой ПС стегоканалов, предназначенных для скрытой передачи информации. Противоборствующая сторона представлена пассивным нарушителем, пытающимся установить факт применения стегосистемы. В этой задаче инфор-мационного скрытия нарушитель не оказывает на стего мешающего воздействия, следовательно, к рассматриваемой стегосисте-ме не предъявляются требования по обеспечению устойчивости к преднамеренному разрушению скрываемых сообщений. Также будем считать, что в процессе передачи стего на него не воздействуют непреднамеренные помехи, следовательно,  .
Под скрытой ПС в рассматриваемых стегосистемах понимается максимальное количество информации, которое необнаружи-ваемым для нарушителя способом потенциально можно встроить в один элемент контейнера и затем извлечь без ошибок. В каче-стве элементов контейнера могут рассматриваться отсчеты звукового или речевого сигнала, дискретизированные в соответствии с теоремой Котельникова, или пикселы подвижного или неподвижного изображения.
Очевидно, что требования по повышению скрытой ПС, необнаруживаемости и устойчивости к удалению и разрушению явля-ются взаимно противоречивыми, улучшить одну характеристику можно только за счет ухудшения других. Поэтому для систем ЦВЗ максимизируется устойчивость к удалению и разрушению водяного знака (максимизируется допустимое искажение D2) при обеспечении сравнительно небольшой пропускной способности и достаточной незаметности, характеризуемой максимально допустимой величиной искажения кодирования D1. В рассматриваемом классе информационно-скрывающих систем максимизи-руется скрытая пропускная способность при обеспечении требуемой необнаруживаемости стегоканала, а к помехоустойчивости предъявляются минимальные требования. Под

4. ОЦЕНКИ СТОЙКОСТИ СТЕГАНОГРАФИЧЕСКИХ СИСТЕМ

И УСЛОВИЯ ИХ ДОСТИЖЕНИЯ

 

4.1. Понятие стеганографической стойкости

 

По сравнению с достаточно хорошо исследованными криптографическими системами понятия и оценки безопасности стеганографических систем более сложны и допускают большее число их толкований [1-3]. В частности, это объясняется как недостаточной теоретической и практической проработкой вопросов безопасности стегосистем,  так и большим разнообразием задач стеганографической защиты информации. Стегосистемы водяных знаков, в частности, должны выполнять задачу защиты авторских и имущественных прав на электронные сообщения при различных попытках активного нарушителя искажения или стирания встроенной в них аутентифицирующей информации. Формально говоря, системы ЦВЗ должны обеспечить аутентификацию отправителей электронных сообщений. Подобная задача может быть возложена на криптографические системы электронной цифровой подписи (ЭЦП) данных, но в отличие от стегосистем водяных знаков, известные системы ЭЦП не обеспечивают защиту авторства не только цифровых, но и аналоговых сообщений и в условиях, когда активный нарушитель вносит искажения в защищаемое сообщение и аутентифицирующую информацию. Иные требования по безопасности предъявляются к стегосистемам, предназначенным для скрытия факта передачи конфиденциальных сообщений от пассивного нарушителя. Также имеет свои особенности обеспечение имитостойкости стегосистем к вводу в скрытый канал передачи ложной информации [4,5].

Как и для криптографических систем защиты информации безопасность стегосистем описывается и оценивается их стойкостью (стеганографической стойкостью или для краткости стегостойкостью).  Под стойкостью различных стегосистем понимается их способность скрывать от квалифицированного нарушителя факт скрытой передачи сообщений, способность противостоять попыткам нарушителя разрушить, исказить, удалить скрытно передаваемые сообщения, а также способность подтвердить или опровергнуть подлинность скрытно передаваемой информации.

В данном разделе рассмотрим определения стегостойкости, опишем классификацию атак на стегосистемы и попытаемся определить условия, в которых стегосистемы могут быть стойкими.

Исследуем стегосистемы, задачей которых является скрытая передача информации. В криптографических системах скрывается содержание конфиденциального сообщения от нарушителя, в то время как в стеганографии дополнительно скрывается факт существования такого сообщения. Поэтому определения стойкости и взлома этих систем различны. В криптографии система защиты информации является стойкой, если располагая перехваченной криптограммой, нарушитель не способен читать

Лабораторная работа № 8. Алгоритмические задачи

1. Определить локальный корень уравнения
   F(x)=x⁷ – 3,5x⁶ + 18,7x⁵ – 64,45x⁴ + 45,67x³ – 159,845x² + 18,285x¹ – 63,9975
   на интервале [-10, 10] методом дихотомии (половинное деление).
2. Определить локальный корень уравнения
   F(x)=x⁷ + 5,6x⁶ + 18,7x⁵ + 104,72x⁴ + 109,92x³ + 615,552x² + 203,58x¹ + 11,48
   на интервале [-10, 10] методом дихотомии (половинное деление).
3. Определить локальный корень уравнения
   F(x)=x⁷ + 4,1x⁶ + 15,1x⁵ + 61,91x⁴ + 64,15x³ + 263,015x² + 79,833x¹ + 327,3153
   на интервале [-10, 10] методом дихотомии (половинное деление)
4. Найти все простые числа от 1 до n, используя алгоритм Эратосфена.
5. Определить НОД(a, b), используя алгоритм Эвклида. НОД(a, b, с)
6. Написать функцию сортировки массива на n элементов по возрастанию, используя шейкер-сортировку (улучшенный метод простого обмена)
7. Написать функцию слияния двух упорядоченных массива в общий упорядоченный массив.
8. Написать функцию поиска числа в одномерном массиве методом половинного деления. Если число не найдено, вернуть -1, иначе — №позиции в массиве.
9. Неориентированный граф задан в виде матрицы смежности. Напишите функцию перевода матрицы смежности в матрицу инциндентности.
10. Неориентированный граф задан в виде матрицы инциндентности. Напишите функцию перевода матрицы инциндентности в матрицу смежности.
11. Неориентированный граф задан в виде матрицы смежности. Напишите функцию перевода матрицы смежности в список ребер.
12. Неориентированный граф задан в виде матрицы инциндентности. Напишите функцию перевода матрицы смежности в список ребер.
13. Неориентированный граф задан в виде списка ребер. Напишите функцию перевода списка ребер в матрицу смежности.
14. Неориентированный граф задан в виде списка ребер. Напишите функцию перевода списка ребер в матрицу инциндентности.
15. Определить все возможные слагаемые для числа х (рекурсивный механизм)
16. Вывести все возможные перестановки для n чисел в лексикографическом порядке
17. Вывести все возможные перестановки для n чисел в антилексикографическом порядке
18. Вывести все возможные сочетания из n чисел по к в лексикографическом порядке
19. Вывести все возможные сочетания из n чисел по к в антилексикографическом порядке
20. Ввести степени и коэффициенты двух многочленов p1(x) и p2(x).    Вычислить и вывести коэффициенты многочлена суммы p1(x) на p2(x)
21. Ввести степени и коэффициенты многочлена p(x).    Вычислить и вывести коэффициенты многочлена, являющегося производной от  p(х).
22. Написать программу, выводящую на экран все двоичные вектора длины m, имеющие заданный вес n <= 4 (рекурсия)
23. Ввести степени и коэффициенты двух

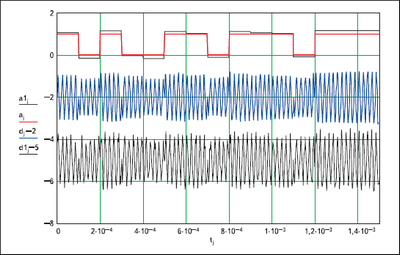
Лабораторная работа включает в себя  5 заданий, выполняемых на ПК с помощью пакета MATLAB.

1. Синтез имитационной модели рекурсивного цифрового фильтра (ЦФ) по заданной форме импульсной характеристики (ИХ).
2. Определение амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ) характеристик синтезированного ЦФ.
3. Определение сигнала на выходе ЦФ при подаче на его вход произвольного сигнала

• с помощью прямой свертки,
• с использованием модели фильтра (коэффициентов фильтра),

• с помощью быстрой свертки (с применением ДПФ).
  Первые три задания выполняются для одной и той же схемы ЦФ.

4. Синтез имитационной модели рекурсивного ЦФ по заданной форме  амплитудно-      частотной характеристики.

5. Синтез имитационной модели рекурсивного ЦФ с помощью программы SPTool.

Задание № 1. Синтез ЦФ по заданной форме ИХ

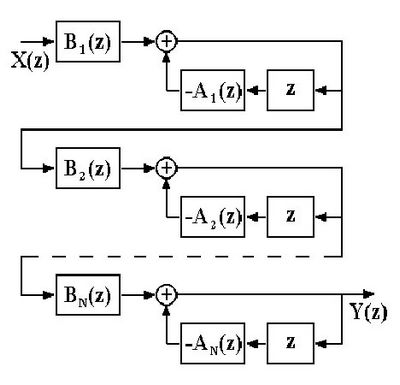
В общем случае ЦФ порядка Nописывается линейным разностным уравнением

,                                        (1)

где x(n) и y(n) – отсчеты входного и выходного сигналов в моменты времени nT (Т = const – период дискретизации сигналов), а_к , b_k – коэффициенты фильтра, постоянные во времени.

Структурная схема ЦФ, реализованного в прямой форме, приведена ниже.

Порядок ЦФ N определяется максимальным числом элементов задержки в прямом или обратном регистрах сдвига.

ЦФ, описываемый уравнением (1), называется рекурсивным. Если все коэффициенты а_к равны 0, то фильтр является нерекурсивным.

Импульсная характеристика h(n) – реакция ЦФ на единичный импульс.

Фильтр с конечной импульсной характеристикой (КИХ-фильтр) – ЦФ, у которого ИХ может принимать отличные от 0 значения на конечном временном интервале. В противном случае фильтр обладает бесконечной ИХ (БИХ-фильтр).

Задается порядок ЦФ N и форма его ИХ на конечном интервале. Определить коэффициенты фильтра a_kи b_k с помощью функции prony(…). Найти реальную ИХ синтезированного фильтра, используя функции filter (…) и  impz(…).

Задание № 2. Определение АЧХ и ФЧХ синтезированного ЦФ

Частотная характеристика (ЧХ)  – комплексная функция, определяется реакцией ЦФ в установившемся режиме на

Тема 1. Простые геометрические формы, трансформация и внешний вид

 

1. Узел Shape  (Форма)

Пример (файл 1-0.wrl): создаётся куб с размерами и цветом/прозрачностью по умолчанию:

2.Базовые примитивы языка VRML (куб, цилиндр, конус, сфера, текст).

2.1. Box (Куб )

Пример (файл 1-1.wrl): создаётся параллелепипед 5.5х3.75х1.0 метров.

2.2. Cylinder (Цилиндр)

Пример (файл 1-2.wrl): создаётся ”ведро” с радиусом основания 2.5 м и высотой 10м.

2.3. Cone (Конус)

Пример (файл 1-3.wrl): создаётся ”колпак” с радиусом основания 5 м и высотой 10м.

2.4. Sphere (Сфера)

Пример (файл 1-4.wrl): создаётся сфера радиусом 3 м.

2.5. Text(Текст) и FontStyle(Стиль текста)

Пример (файл 1-5.wrl): создаётся текст  (2 строки).

3. Трансформация объектов

Узел Transform (Трансформация).

Пример (файл 1-6.wrl): создаётся несколько объектов (3 объекта), одна из групп (2 объекта) объектов масштабируется, вращается и смещается, с третьим объектом никаких действий не производится .

4. Внешний вид

Узел Appearance (Внешний вид).

4.1 Узел Material (материал)

Пример (файл 1-7.wrl): можно наблюдать полупрозрачный зелёный параллелепипед на фоне серой(по умолчанию) сферы.

4.2. Наложение текстур.

4.2.1. ImageTexture (Текстура-изображение)

Пример (файл 1-8.wrl): иллюстрирует наложение текстуры на сферу.

4.2.2. MovieTexture (Движущаяся текстура)

Пример (файл 1-9.wrl): на грани параллелепипеда накладывается текстура.

4.2.3. PixelTexture

Пример (файл 1-10.wrl): куб и сфера раскрашиваются текстурой 2х2 пикселя вида

4.3. Трансформация текстур

Узел  TextureTransform (Трансформация текстуры)

Пример (файл 1-11.wrl):

 

Тема 2. ПРЕДСТАВЛЕНИЕ СЛОЖНЫХ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ

 

1. PointSet (Набор точек)

Color (Цвет).

Coordinate (Коодинаты)

Пример (файл 2-3.wrl) : создаются 8 разноцветных точек в пространстве.

2. IndexedLineSet (Индексированный набор линий)

Пример (файл 2-2.wrl) : рисуются 2 многоугольника, образующих 2 перпендикулярные плоскости. Значения цветов в вершинах линий интерполируются по поверхностям линий.

3. IndexedFaceSet (Индексированный набор поверхностей)

Normal (Нормаль)

Пример (файл 2-1.wrl) : определяется 4 полупрозрачные плоскости (видимые с двух сторон), определяющие ½ куба. Цвета соответствуют вершинам (интерполируются между ними).

Пример (файл 2-1-1.wrl) : определяется 4 плоскости, каждая видна только с одной стороны. Цвета соответствуют вершинам

1. ПоНятие аЛГоритМа
В своей профессиональной деятельности выпускники ГУаП решают самые разные задачи. Среди этих задач встречаются такие,
методы решения которых известны, и требуется лишь правильно
их использовать. однако развитие науки и техники приводит к необходимости создавать новые методы решения новых задач.
что же такое метод известно определение (конечно, шуточное):
метод – это искусственный прием, примененный дважды. Но тогда разработка методов – это не наука, а искусство, и не существует
правил, зная которые, можно найти решение для любой задачи.
а если такие правила все-таки существуют Существуют, естественно, правила решения многих задач. еще в средней школе мы
узнали, как сложить или перемножить два любых рациональных
числа, как поделить их друг на друга с любой точностью, как найти
наибольший общий делитель двух целых чисел. Эти правила известны с давних времен. курс математического анализа знакомит
нас с правилами дифференцирования элементарных функций и интегрирования некоторых элементарных функций.
очевидно, что множество этих задач делится на классы однотипных: задачи одного класса различаются лишь параметрами и
решаются единообразно. каждый такой класс называют массовой
проблемой.
определение. общий, единообразный, точно определенный способ решения любой задачи из данного класса называется алгоритмом.
Это определение, безусловно, не является математически строгим и носит интуитивный характер, поскольку включает в себя
слово «способ», смысл которого не определен ранее.
Слово «алгоритм» происходит от имени персидского математика и астронома IX в. абу Джафара аль-Хорезми, написавшего
трактат по математике «китаб аль-джебр валь-мукабала» («книга
о восстановлении и противопоставлении»). В XII в. трактат переведен с арабского на латинский язык. Слово «алгебра» происходит от
названия математической операции «аль-джебр».
очевидно, что очень важно знать, для каких классов задач существуют алгоритмы решения, а для каких не существуют. Вопрос
этот приобрел особую значимость в минувшем веке, когда появилась кибернетика, стали разрабатывать и применять вычислительные машины. Поскольку в то время вычисления являлись привелегией людей и считались наиболее сложным видом мыслительной
деятельности, интерес представлял философский вопрос: может
ли машина мыслить если это возможно, то перед человечеством
открываются невиданные перспективы, но одновременно появляются и серьезные опасности. если это невозможно, то хорошо бы
знать, что может машина, и научить ее мыслить.
однако когда мы говорим о задачах, требующих решения, то
имеем в виду не только задачи, возникающие на практике. На рубеже XIX–XX вв. математика достигла той ступени развития, на
которой остро

Введение

Практически все современные системы трехмерной графики используют концепцию так называемого графического конвейера
(Graphic Pipeline), представляющего собой логически связанную последовательность (или группу) вычислений, которые синтезируют на
выходе системы образ пространственной сцены. Конвейер разделен
на ряд этапов, на каждом из которых аппаратно или программно выполняется некоторая функция. Реализация конвейера может быть
полностью программной, полностью аппаратной или смешанной
(программно-аппаратной). Обычно в структуре графического конвейера выделяют ряд последовательных этапов обработки исходной
пространственной сцены. В частности, в данном случае будем придерживаться достаточно традиционной структуры (см., например
[5]). Пример конвейера, разделенного на два стадии: геометрические
преобразования и рендеринг приведен на рис. 1.
Указанные стадии процесса создания изображений на экране
монитора связаны между собой достаточно прочно, и ни одна из
них в отдельности не может привести к созданию достаточно реалистичных графических объектов.
Разделы пособия будут посвящены методам, чаще других используемым для реализации каждого из представленных на рис. 1
этапов.
здесь же, во введении кратко рассмотрим каждую из стадий графического конвейера с тем, чтобы понять, о чем собственно пойдет
разговор.

Геометрические преобразования
Первый этап (моделирование) состоит в аппроксимации трехмерных объектов пространственной сцены, которые в общем случае представляют собой криволинейные поверхности множеством
многоугольников (полигонов). Отсюда термин – «полигональная
аппроксимация поверхности». Чаще всего в качестве таких полигонов используются треугольники (как самые простые полигоны).
Следует учитывать, что, чем мельче полигоны, тем ближе аппроксимация к модели, но и тем более громоздким становится описание
объекта, а, следовательно, и больше времени требуется на его обработку. Представление криволинейной поверхности совокупностью
плоских граней-полигонов c точностью, достаточной для имитации гладкой поверхности, называется тесселяцией (tesselation), а
в случае, когда в качестве таких полигонов выступают простейшие
многоугольники – треугольники, применяется термин триангуляция (triangulation). Множество таких полигонов (сотни, а иногда
и тысячи) соединяются друг с другом и образуют сложные трехмерные сетки. В качестве достойной альтернативы полигональной
аппроксимации в последнее время в графических конвейерах все
чаще выступают методы моделирования гладких поверхностей, использующие для этой цели кривые (поверхности) безье или сплайны. Причем вычислительные мощности современных компьютеров
возросли настолько, что позволяют отображать такие

Освоение приемов работы со шрифтами
в программе Corel Draw
После загрузки программы на экране Вы увидите контур
чистого листа, на котором можно писать и рисовать.

Ч. 1. Фигурные шрифты. Организация фигурного текста и его окраски
•Выберите инструмент “Текст” (Рис. П. 1.1) и щелкните*
мышью по листу там, где Вы хотите расположить текст.
•введите текст “Курсы по рек
ламе”;
•выберите инструмент “Указатель”: текст будет окружен
восьмью маркерами;
•в панели свойств откройте
список шрифтов и выберите
“Arial.Суг”;
• установите размер шрифта
24 пункта;
•выберите указателем любой

Текст
Интерактивное
перетекание

Рис. П. 1.1. Инструменты
Corel Draw

маркер и измените масштаб фразы (текст оставьте горизонтальным);
•установите указатель в центр рамки и поместите текст
симметрично внутри контура листа;
•измените цвет текста, выб
рав его в палитре указателем, в
случае необходимости увеличьте число доступных цветов, щелкнув по кнопке, расположенной
под палитрой (Рис. П. 1.2);
•сделайте обводку букв текста: выберите инструмент “Аб
Развернуть палитру
Рис. П. 1.2. Фрагмент
палитры

рис” и в нем “Диалог цвета абриса”; в открывшемся диалого

*“Щелкнуть мышью по листу” – означает подвести курсор к нужной точке на экране, а затем нажать и отпустить кнопку мыши.

Обновить цветовую ссылку
Рис. П. 1. 3. Фрагмент диалогового
окна “Цвет абриса”

вом окне выберите необходимый цвет и нажмите
кнопку “Обновление цветовой ссылки” (рис. П. 1.3);
закройте диалоговое окно;
• установите жирный
шрифт;
• выделите первую
букву: для этого выберите инструмент “Фигура”,
два раза щелкните мышью по тексту; под каждой буквой появятся точки; нацельте указатель на
точку под первой буквой,

нажмите левую кнопку мыши и переместите букву вверх
или вниз; отпустите кнопку мыши;
•измените цвет выделенной буквы, выбрав его в палитре
указателем;
•измените размер выделенной буквы, установив требуемый размер шрифта в панели свойств;
• выберите инструмент “Фигура”; удерживая клавишу
“Shift”, выберите несколько букв (щелкая мышью по маркерам – точкам под буквами) и сместите выделенное;
•выберите инструмент “Указатель”, выделите весь текст;
•нажмите кнопку “Преобразовать в кривую” в панели
свойств, затем нажмите кнопку “Разгруппировать все”
(рис. П. 1.4);
•выберите инструмент “Фигура”, щелкните мышью по
тексту: обозначатся узлы букв;
•увеличьте масштаб столь
сильно, чтобы узлы не слива
Редактировать текст

лись;
• удерживая клавишу
“Shift”, выделите узлы нижнего элемента буквы “Р”;
• захватите любой из вы
Форматировать
текст

Преобразовать
в кривые

деленных узлов и перемещайте его (если нажата клавиша
“Ctrl” перемещение возмож

Рис. П. 1.4. Панель свойств
объекта “Текст”

но только по горизонтали

Основные приемы ретуширования изображений
Программа Adobe Photoshop обеспечивает Вас рядом инструментальных средств и команд, с помощью которых Вы сможете улучшить качество фотографических изображений. Этот
урок объясняет основные методы для исправления изображения. Делая последовательные шаги, Вы постепенно овладеете
основными приемами изменения размеров, положения, ретуширования фотографий, предназначенных для печати.
Вы научитесь делать следующее:
¦Выбирать правильную разрешающую способность для
редактируемой фотографии.
¦Обрезать (кадрировать) изображение.
¦Корректировать тоновый диапазон изображения.
¦Удалять оттенки цвета из изображения, используя корректировку слоев.
Использовать команду “Замена цвета”, чтобы изменить цветовой тон и насыщенность выбранного цвета в фотографии.
¦ Корректировать насыщенность и яркость изолированных областей изображения, используя губку (изменение
насыщенности) и инструменты “затемнение” и “осветление”.
¦ Использовать инструмент “штамп”, чтобы устранить
нежелательный объект из изображения.
¦Заменять части изображения другими изображениями.
¦Применять фильтр – нерезкое маскирование (“Снять
резкость”), чтобы повысить резкость изображения и на этом
закончить процесс фоторетуширования.
¦ Сохранять файл Adobe PhotoShop в формате, который
может использовать программа.
Стратегия ретуширования
В программе Adobe PhotoShop Вы можете ретушировать
фотографические изображения способами, которые ранее
были доступны только высоко квалифицированным профессионалам. Вы можете исправлять проблемы качества цвета
и тонового диапазона изображения, возникшие в оригинале
фотоснимка при фотосъемке или при сканировании изображения. Вы можете также исправлять композицию и плохую
фокусировку изображения.

Основные шаги
Проведению ретуширования в программе Adobe PhotoShop
предшествуют следующие общие шаги:
Рис. П. 5.1. Начало и окончание Вашей работы над фотографией
для обложки журнала

¦Проверяют качество сканирования и удостоверяются,
что разрешающая способность соответствует той, которая
должна быть использована в итоговом изображении.
¦Обрезают (кадрируют) изображение.
¦ Корректируют общий контраст или тоновый диапазон
изображения.
¦Устраняют ложный цветовой оттенок (когда изображение “уходит” в какой-то неверный цветовой тон).
¦Корректируют цвет и тон в специфических частях изображения, чтобы проявить малонасыщенные цвета в областях светлых и средних тонов, а также в тенях.
¦Повышают общую резкость изображения.
Ретушь изображений для различных применений
Методы ретуширования, которые Вы примените к изображению, в определенной степени зависят от того, как будет
использоваться изображение. Предназначено ли изображение
для

Введение

Многие отрасли техники, имеющие отношение к получению, об
работке, хранению и передаче информации, в значительной степени
ориентируются в настоящее время на развитие систем, в которых
информация имеет характер изображений. Изображение, которое
можно рассматривать как двумерный сигнал, является значительно
более емким носителем информации, чем обычный одномерный, чаще
всего временной, сигнал. Вместе с тем, решение научных и инженер
ных задач при работе с визуальными данными требует особых уси
лий, опирающихся на знание специфических методов, поскольку
традиционная идеология обработки и анализа одномерных сигналов
мало пригодна в этих случаях.
Одной из основных проблем, возникающих при обработке изобра
жений, является улучшение качества изображения, в частности,
повышение различимости отдельных фрагментов. К причинам, по
нижающим качество изображений, можно отнести:
технические яркостные помехи шумового характера;
недостаточная или излишняя освещенность объектов съемки;
отсутствие резкости при получении изображения;
слишком мелкие размеры деталей, которые необходимо разли
чить.
Основной целью компьютерной обработки изображений является
нахождение таких методов, результат работы которых оказался бы
более подходящим с точки зрения конкретного применения. Когда
изображение обрабатывается для визуальной интерпретации, наблю
датель является окончательным судьей того, насколько хорошо дей
ствует конкретный метод. Визуальное оценивание качества изобра
жения является крайне субъективным процессом, делающим поня
тие «хорошего изображения» некоторым абстрактным эталоном,
с помощью которого необходимо сравнивать эффективность алгорит
мов. Если целью является обработка изображения для восприятия
другими компьютерными программами, то проблема оценивания не
сколько упрощается. Например, в задаче распознавания символов
наилучшим будет тот метод обработки изображений, который дает

более точные результаты компьютерного распознавания. Тем не ме
нее, даже в ситуации, когда проблема позволяет установить четкие
критерии качества, обычно требуется некоторое количество попы
ток тестирования, пока не будет выбран конкретный метод.
Множество методов улучшения качества изображений распадает
ся на две большие категории: методы обработки в пространственной
области и методы обработки в частотной области. Термин «простран
ственная область» относится к плоскости растрового изображения,
состоящего из отдельных пикселей, и объединяет методы, основан
ные на прямом манипулировании пикселями изображения. Методы
обработки в частотной области основываются на модификации сиг
нала, формируемого путем применения к изображению преобразова
ния Фурье