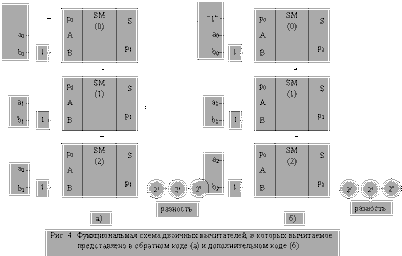
орграфом.
Имея в своей основе простейшие идеи и элементы (точки, соединенные линиями), теория графов строит из них огромное многообразие форм,
наделяет эти формы различными свойствами и в результате становится полезным инструментом при исследовании самых разнообразных систем.
В самом понятии графа сочетаются теоретико-множественные, комбинаторные и топологические аспекты, что делает теорию графов удобным, простым языком для формулировки и построения моделей, а также эффективным и мощным инструментом решения задач, относящихся к широкому кругу научных и инженерных проблем. Можно упомянуть в этой связи вопросы конструирования сиcтем автоматизированного проектирования, систем программирования для ЭВМ и создания
операционных систем, исследования операций и управления, математической лингвистики и разработки трансляторов, календарное планирование промышленного производства, задачи сетевого планирования и
управления (СПУ), тактические и логические задачи выбора лучших
объектов, большой круг экономических задач, игровые задачи.
Вместо понятия графа часто используется понятие сеть, когда кроме основных, чисто структурных, отношений в графе задаются некоторые количественные характеристики точек и линий. При этом можно
решать проблемы построения электрических сетей, систем связи и исследования процессов передачи информации, выбора оптимальных маршрутов и потоков в сетях, например построения сети выполнения работ при проектировании изделия. При этом ребрам или (и) дугам сети
Цель данного курса состоит в том, чтобы ознакомить студентов с
основными понятиями теории графов и первыми представлениями о
моделях теории графов, их приложениях к решению некоторых прикладных задач с использованием алгоритмического подхода и с возможностью применения ЭВМ.
1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ПОНЯТИЯ
Для определения основных понятий теории графов будут использованы некоторые сведения из теории множеств. Множество образуется совокупностью дискретных объектов, являющихся элементами
множества, и обозначаются A = {a, b, c }, где a, b, c элементы
множества A.
Предполагается, что для