Лабораторная работа включает в себя 5 заданий, выполняемых на ПК с помощью пакета MATLAB.
- Синтез имитационной модели рекурсивного цифрового фильтра (ЦФ) по заданной форме импульсной характеристики (ИХ).
- Определение амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ) характеристик синтезированного ЦФ.
- Определение сигнала на выходе ЦФ при подаче на его вход произвольного сигнала
- с помощью прямой свертки,
- с использованием модели фильтра (коэффициентов фильтра),
- с помощью быстрой свертки (с применением ДПФ).
Первые три задания выполняются для одной и той же схемы ЦФ.
4. Синтез имитационной модели рекурсивного ЦФ по заданной форме амплитудно- частотной характеристики.
5. Синтез имитационной модели рекурсивного ЦФ с помощью программы SPTool.
Задание № 1. Синтез ЦФ по заданной форме ИХ
В общем случае ЦФ порядка Nописывается линейным разностным уравнением
, (1)
где x(n) и y(n) – отсчеты входного и выходного сигналов в моменты времени nT (Т = const – период дискретизации сигналов), ак , bk – коэффициенты фильтра, постоянные во времени.
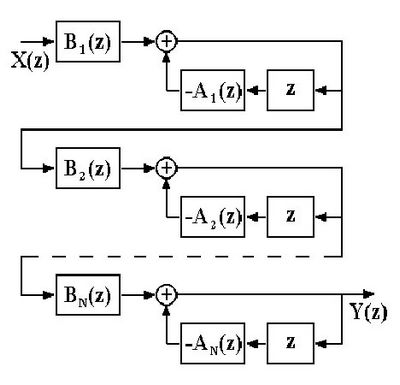
Структурная схема ЦФ, реализованного в прямой форме, приведена ниже.
Порядок ЦФ N определяется максимальным числом элементов задержки в прямом или обратном регистрах сдвига.
ЦФ, описываемый уравнением (1), называется рекурсивным. Если все коэффициенты ак равны 0, то фильтр является нерекурсивным.
Импульсная характеристика h(n) – реакция ЦФ на единичный импульс.
Фильтр с конечной импульсной характеристикой (КИХ-фильтр) – ЦФ, у которого ИХ может принимать отличные от 0 значения на конечном временном интервале. В противном случае фильтр обладает бесконечной ИХ (БИХ-фильтр).
Задается порядок ЦФ N и форма его ИХ на конечном интервале. Определить коэффициенты фильтра akи bk с помощью функции prony(…). Найти реальную ИХ синтезированного фильтра, используя функции filter (…) и impz(…).
Задание № 2. Определение АЧХ и ФЧХ синтезированного ЦФ
Частотная характеристика (ЧХ) – комплексная функция, определяется реакцией ЦФ в установившемся режиме на
