В лабораторной работе требуется получить случайную последовательность чисел в соответствии с вариантом. Оценить эффективность алгоритма.
Наиболее известными вероятностными моделями являются модели теории массового обслуживания и статистической физики. Компьютерное моделирование позволяет воспроизводить поведение таких моделей во времени на ЭВМ. При этом выполняются следующие действия:
-выбирается реализации случайных чисел с помощью ДСЧ;
-с помощью этих чисел получаются реализации случайных величин и процессов с более сложными распределениями;
-вычисляются характеристики модели;
Рассмотрим некоторые способы генерации потоков случайных величин.
Часть I.
1.1 Моделирование дискретных случайных величин .
Основан на соотношении ,
где , m=0,1…,
,
1.1.1 Табличный способ.
Накопительная вероятность задается таблицей распределения.
1.1.2 Посредством рекуррентных соотношений.
Используется для формирования дискретных случайных величин с распределением Рк. При этом вероятность появления числа k+1 может определяться рекуррентно , где r(k) =Pr+1/Pk .
Эффективность алгоритма обратно пропорциональна числу арифметических операций для моделирования
(для целочисленной )
1.2 Специальные методы.
В некоторых случаях можно увеличить эффективность алгоритма,
Рассмотрим метод вычитания по убыванию номера. При этом изменяют порядок проб для определения интервала, в который попадает . Алгоритм применяется для моделирования случайных величин, имеющих моду.
Чтобы воспользоваться этим методом, необходимо знать точку максимальной вероятности .
Тогда для заданного значения осуществляется проверка
(где для распределения Пуассона).
Затем пробы для определения m производятся по возрастанию k, начиная с l+1, если соотношение =t, или по убыванию, начиная с l,
II. Моделирование непрерывных случайных величин.
2.1 Метод обратной функции.
Пусть , где — строго монотонная, непрерывная функция на интервале (0,1), задана.
Тогда для
.
Или для
для
Алгоритм моделирования случайной величины следующий:
1. Генерируем случайную величину , имеющую равномерное распределение на интервале (0,1).
2. Решаем уравнение x=F-1() или x=F-1(1-), где х – искомая случайная величина с заданным законом распределения.
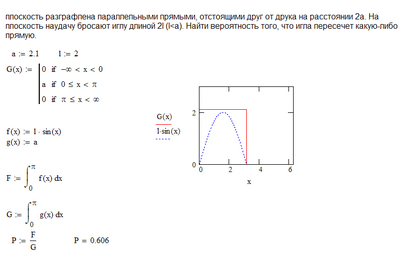
2.2 Метод режекции Дж. фон Неймана.
Используется , если
Пусть заданы g(x) итакие, что и . Пусть также существует метод моделирования для плотности .
Тогда алгоритм для включает следующие действия:
1) Выбирается случайно точка , где равномерно распределена в области .
2)
