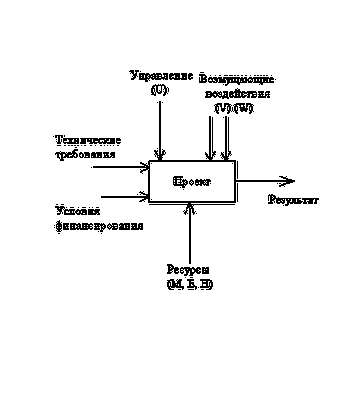
Постановка задачи. Для выполнения курсового проекта необходима компьютерная модель «чёрного ящика» – преобразователя вектора Х входных воздействий с аддитивной погрешностью (рис.1).
Исходные данные.
- Функция Y=F(X).
- Вид распределения.
- Параметры распределения.
- Моменты распределения
Моделирование погрешности произвольного непрерывного распределения на основе датчика независимых с.ч. равномерного распределения.
Метод обратной функции.
Метод режекции.
Моделирование нормального распределения.
Моделирование распределения Эрланга.
Вид распределения задается функцией распределения F(x) или плотностью распределения f(x).
x
F(x)=∫ f(x)dx .
-∞
∞
F(x)=∫ f(x)dx =1.
-∞
Параметры распределения – константы аналитического выражения функции распределения. Иногда параметрами распределения являются моменты, например, в нормальном распределении параметрами являются математическое ожидание и дисперсия.
По известным моментам можно определить параметры.
Моменты –
начальные n-порядка b
µ=∫ xn f(x)dx
a
центральные n-порядка b
εn=∫ (x-m)n f(x)dx
a
Математическое ожидание b
m=∫ x1 f(x)dx
a
Дисперсия b
Ɛ=∫ (x-m)2 f(x)dx
a
Метод обратной функции.
Пусть , где — строго монотонная, непрерывная функция на интервале (0,1), задана.
Тогда для
.
Или для
для Доказательство [1 ст.19]
Алгоритм моделирования случайной величины следующий:
1. Генерируем случайную величину , имеющую равномерное распределение на интервале (0,1).
2. Решаем уравнение x=F-1() или x=F-1(1-), где х – искомая случайная величина с заданным законом распределения.
Метод режекции Дж. фон Неймана.
Используется , если
Пусть заданы g(x) итакие, что и . Пусть также существует метод моделирования для плотности .
Тогда, алгоритм для включает следующие действия:
1) Выбирается случайно точка , где
