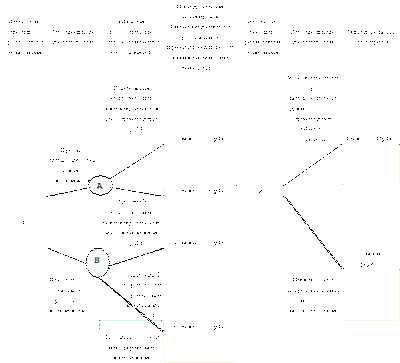
Постановка задачи.
Есть модель технологического процесса в виде «черного ящика» (ч.я.) (рис.1). На вход ч.я. подаётся n-мерный вектор Х (х1,х2,…,хn) входных воздействий. На выходе измеряется отклик , представленный в виде числа, с аддитивной погрешностью . Необходимо построить уравнение регрессии в виде полинома , с заданной точностью .
Х
Рис.1 Модель черного ящика.
Исходные данные.
- Модель ч.я.
- Диапазон значений вектора входных воздействий.
- Точность аппроксимации.
Алгоритм выполнения задания.
- Планирование и проведение эксперимента.
1.1. Определить вид полинома.
1.2. Сформировать матрицу планирования А.
1.3. Провести компьютерный эксперимент в соответствии с данными матрицы планирования. В каждой точке плана проводится не меньше 12 экспериментов, в этом случае отклик имеет асимптотически нормальное распределение.
- Обработка результатов эксперимента.
2.1. Вычислить средний отклик в каждой точке плана. Заполнить матрицу А.
2.2. Вычислить коэффициенты полинома. Вычислить отклики, даваемые уравнением регрессии.
2.3. Проверить построенное уравнение регрессии на адекватность. В случае, если уравнение не удовлетворяет критерию адекватности, вернутся на п.1, дополнив полином.
2.4. Проверить точность аппроксимации. Если точность неудовлетворительна, вернуться на п.1, дополнив полином.
2.5. Провести факторный анализ модели.
- Выводы.
Краткий список используемых обозначений.
- N – число повторений опыта в каждой точке плана
- n – число слагаемых в уравнении регрессии
- m – число факторов (размерность входного вектора Х)
- t – число точек в плане
- k – число генераторов в ДФП
- — средний отклик, даваемый экспериментом
- — отклик, даваемый уравнением регрессии
- — транспонированная матрица планирования.
- Θ – неизвестные коэффициенты уравнения регрессии.
- — оценки неизвестных коэффициентов регрессии
Указания к выполнению задания.
Общие замечания.
Будем использовать следующие термины:
— фактор – переменная, влияющая на отклик. Факторами являются входные переменные модели х1,х2,…,хn, образующие вектор Х входных переменных;
— план эксперимента – область определения Х;
— точка в плане эксперимента – означенный вектор Х;
— аппроксимирующий полином – некоторая бесконечная последовательность вида
Например, полином с двойными взаимодействиями и тремя факторами имеет вид
,
под взаимодействием понимается произведение факторов.
Необходимое количество точек в плане эксперимента,
