Лабораторная работа № 1
МодеЛирование сЛучайных процессов
МетодоМ форМирующего фиЛьтра
Цель работы – изучение и освоение навыков практического применения метода формирующего фильтра для имитации нормальных случайных процессов, обладающих заданными корреляционными характеристиками.
Методические указания, основные понятия
Моделированию в лабораторной работе подлежит нормальный
случайный процесс h(t) на временном интервале [0, T]. Корреляционная функция процесса h(t) может быть задана в непрерывной K(t)
или дискретной K n[ ]= K n t( ) форме, где t T N – шаг дискретизации, равный отношению длительности временного интервала T к
общему числу временных отсчетов N.
Для имитации на ЦВМ случайного процесса h(t) наиболее часто
используется очевидный прием, состоящий в линейном преобразовании исходного дельта-коррелированного случайного процесса
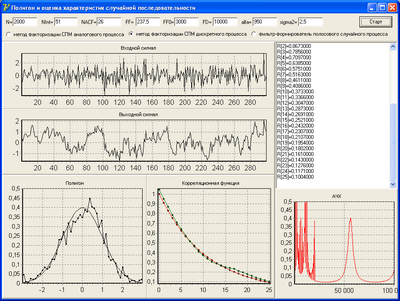
(белового шума) с помощью дискретного фильтра, параметры и начальные условия которого выбираются исходя из требуемой функции K(t). Этот прием иллюстрирует рис. 1, где показаны примеры
реализации x[n] исходного дельта-коррелированного случайного
процесса и формируемой реализации y[n] процесса h(t), являющейся откликом блока фильтрации – формирующего фильтра.
Итак, формирующий фильтр –динамическое звено, преобразующее
случайный процесс вида белого шума в случайный процесс с заданными корреляционными (или спектральными) характеристиками.
Реализация формирующего фильтра возможна как во временной, так и в частотной области. Как правило, предпочтение отдается тому способу, который приводит к наименьшей вычислительной сложности конечного моделирующего алгоритма, либо требует
наиболее простых подготовительных действий по идентификации
дискретной передаточной функции формирующего фильтра.
Структурная схема, представляющая АРСС-модель в виде рекурсивного дискретного фильтра, показана на рис. 2. Из этого рисунка
видно, что алгоритм (1) описывает замкнутую линейную дискретную систему, содержащую прямую и обратную цепи.
Выделяют два важных частных случая общей модели (1).
1. Модель скользящего среднего. В данном случае все коэффициенты bl (l=1, …, L) равны нулю, т. е.
I
[ ]= е a x n ii [ — ] (2)
i=0
где I – порядок модели скользящего среднего.
Иногда такую модель называют чисто нулевой моделью, поскольку передаточная функция соответствующего дискретного фильтра
имеет только нули, а сам фильтр является нерекурсивным (на рис. 2
отсутствует цепь обратной связи).
Способы нахождения весовых коэффициентов {ai} по заданной
корреляционной функции стационарного случайного процесса подробно рассматриваются в [3, 11]. Из числа этих способов разложение функции спектральной плотности в ряд Фурье наиболее удобно для использования в современных математических программах,
